I can answer this one.
An object will always tip over when the center of gravity is outside of its outermost support. Here is a diagram to clarify.
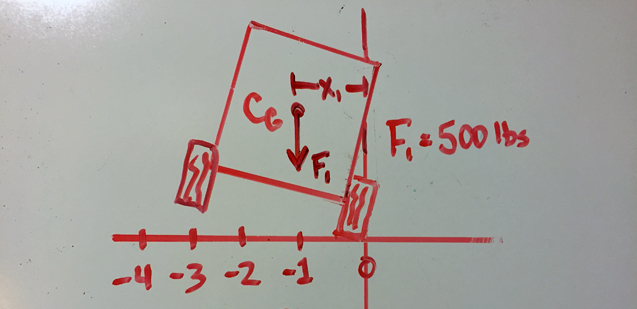
We can see that the center of gravity is still on the correct side of the tire about which it is tipping. The force of gravity (noted as F1) will right this trailer and it will land on its wheels.
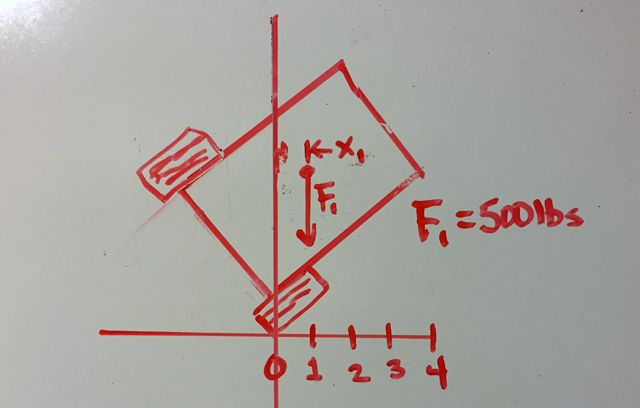
In this diagram we can see that the center of gravity is on the wrong side of the tire about which it is tipping. Gravity is going to tip this trailer onto its side. Sorry my labeling of X1 is so messy.
So here is where the common rules of thumb come into play. The wider the trailer is, the harder it is to tip it so far that the center of gravity passes the outside support. Also, if the center of gravity is very low, this makes it harder to tip the trailer so far that the CG passes the outside support. To sum up: if you don't want your vehicle to tip, make it wide and keep the center of gravity low. But that's not very helpful because it doesn't give you numbers you can work with to predict when your trailer might tip. So let's look at another diagram.
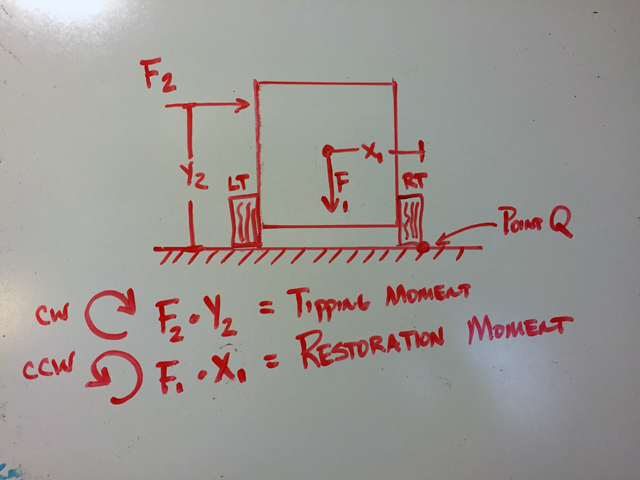
In this diagram F2 is the force due to the wind. The wind applies force to the whole side of the trailer but it can be summed up as a single force acting through a single point. It is acting through point Y2. F2 x Y2 creates a moment (which is just a word that means twisting force) and that twisting force wants to tip the trailer about point Q. (This assumes the tire isn't going to just side which is probably a good assumption) Let's call this moment the "tipping" moment.
F1 is the force due to the weight of the trailer and it is acting through its center of gravity which is at X1. F1 times X1 creates a moment that wants to keep the trailer on its tires. Let's call this moment the "Restoration" moment.
So as long as the restoration moment is greater than the tipping moment, all is well and the trailer stays safely on its tires. When the moments are equal then it is the start of danger so let's try to find out when that occurs.
Let's look at the variables in question:
X1 is the horizontal distance from the center of the trailer to the outside of the tire (in ft), assuming that you build your trailer symmetrically so that the center of gravity isn't skewed to one side of the trailer. I think I chose the center of the tire for my calcs.
F1 is the weight of the trailer in lbs.
Y2 is the point through which all of the summed up wind forces acts (in ft). This can be tricky to determine for anything other than a simple shape (such as a box). What you want to find is the centroid of the shape. If you use something like SketchUp to draw your designs, there is a way to let it find the centroid for you. Anyway.... for our example let's assume you are building a box trailer. The centroid would be at 1/2 the height of the box.
F2 is the force due to the wind. This one is complex enough that I'll explain it below.
F2 = Area of the side of the trailer x Pressure from the wind x The coefficient of drag of the trailer side. In condensed form it looks like this: F2 = A x P x Cd
The area of the side of the trailer is calculated in square feet. Again this get's tricky if you have something other than a simple shape. This is another value that I let SketchUp calculate for me. For a box trailer it would simply be width x height
The pressure from the wind is calculated by this equation:
P = 0.00256 x V^2 (That's a number, 0.00256 times the velocity of the wind squared) where velocity is measured in miles per hour.
Finally Cd is the coefficient of drag for your shape. This is another tricky variable to define. It totally depends on the shape and it has to be determined in a wind tunnel. The best you can do is estimate it based on some of the values in the table below.
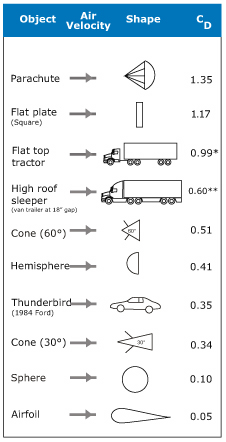
So at this point it would be wise to put all of this in a spreadsheet so that you can play with the numbers. But what you really want to know is "At what point does the left side of the equation below equal the right side"
F1 x X1 = A x 0.00256 x V^2 x Cd x Y2
I was going to put some example numbers in but I'm not sure that would be all that helpful. It comes down to playing with Trailer weight, trailer width, surface area of the side of the trailer, trailer height (because a taller trailer will have a larger Y2 value), wind speed and picking a Cd. I chose 1.17 as a value but only because I was pretty sure my trailer shape would have a lower Cd than that. I like to know the worst case scenario.
Anyway... I hope that my explanation was helpful.








