tongue strength- angle verses square tube

[type82e]

ive just built a little utility trailer for my mower and used 2" * 2" * 1/6" angle in an a frame for the draw bar
and when i checked out andrews tongue strength calculator http://www.angib.pwp.blueyonder.co.uk/t ... tear00.htm

the way I read it is that square tube of the same weight is nearly 3 times stronger than angle? is that right?

ie. 2" * 2" * 1/4" angle has a section modulas of 0.188 and 2" * 2" * 1/8" square tube which has the same ammount of steel in it has a section modulas of 0.511?
marcel

[angib]

1) Errrr, dammit, this is embarassing.

To write this, I looked again at the numbers for angles on this web page and found an error. The weights and strengths of the angles have gone up a bit. The 2" x 2" x 1/4" angles now weighs 3.19 lb/ft (which checks with Online Metals) and has a section modulus of 0.245 in3.

Sorry. The difference remains - it's just a bit smaller. The web page has been updated.

2) Angles are fairly inefficient structural members in bending, whereas square tubes are really good. So for the same weight, tubes are stronger.

If you want the tech-y explanation, it's like this:
The problem with angles is that they are not symmetrical, so one side fails long before the other side is fully loaded. When bending anything, there's a point on its cross section where the stress is zero (ie, neither in compression nor in tension) - it's called the neutral axis. I find it easiest to think of the neutral axis as the 'centre of gravity' of the section (which it is). For a tube the neutral axis is in the middle, but in an angle it's much nearer the flat:


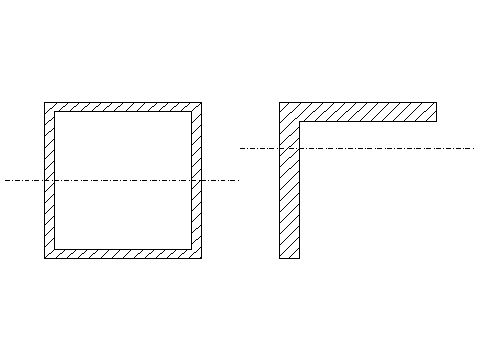
That's real data for a 2" x 2" x 1/8" tube and a 2" x 2" x 1/4" angle.

So when the angle reaches its maximum load, just before it fails, the tip of the bottom leg will be at the maximum stress, but the other leg is less than half as far from the neutral axis and so it is at less than half the maximum stress, so it's not carrying much load.

Is that clear? There will be questions later.....

Andrew

[type82e]

thanks for that great info!
so i would be better off to weld the 2 angles together and just have one single drawbar up the middle as it would still be twice as strong as the 2 single angles?
the reason I'm using angle is that I had some left over bits that ive collected
marcel

[angib]

so i would be better off to weld the 2 angles together and just have one single drawbar up the middle as it would still be twice as strong as the 2 single angles?

Yes and no!

If you weld two 1/4" angles together, you'll get a section modulus of about 0.91 in3, which is indeed close to twice the 0.49 in3 that the two angles would give if used separately.

However you now have only a central tongue, so you need to add enough transverse structure to carry the tongue load out to the side of the frame - there's no point having a strong tongue that's attached to a wobbly frame.

A-frame tongues also have the advantage that their shape means that lateral tongue loads (sway, etc) produce very little stress because the A-frame is so strong in that direction. However vertical tongue loads remain the critical load for a tongue.

Andrew

[st]

If its a small trailer as you say, it should be fine. There are commercially trailers around here that have survived for a long time (like my fathers) and use similar member dimensions.

I wouldn't 'box' and go to single beam out front for reasons Andrew mentioned. If you box the A frame it would stiffen it by a factor well over 2, and could be done if you wish, but I doubt it's necessary. When looking at just comparisons, its easy to want/need/have to go for the biggest and strongest even if its not necessary.

[cracker39]

OK, Andrew. My lack of knowledge re metals has me baffled again. You mentioned the weight per foot of a particular size metal. You also mentioned online metals. I went to www.onlinemetals.com, which I assume that you were referencing. At the calculator page, I was asked to choose an alloy and didn't know what type. But, as I was selecting Steel as the material, it seemed not to matter about the alloy type. All alloys calculated the same at 4.6 lbs per foot for 2"x2"x3/16". Does that sound correct? I think I got it right. But, I didn't see a selection for angle. I suppose that angle would weigh roughly one half of square tubular for the sale wall width and thickness. Now, I can calulate my trailer chassis weight. Thanks for the tip.

[cracker39]

No longer baffled I think. I ran a spreadsheet with weights of the steel from Online Metals, and weights of an axle, hubs, tires and wheels from NT. The latter are shipping weights. My estimated total weight for the 5'x9' chassis is 345 lbs. The side rails and 3 cross members are of 2x2x1/8 tube. As the span between cross members is over 4 ft, I added two 1x2x1/8 angle cross members to help support the floor. The A frame tongue is 2x2x3/16. The rear bumpers are also 2x2x1/8 angle and only contribute 20 lbs to the total weight. Considering the weights i've seen of some TD 4x8 chassis', I don't think that is too much weight for a chassis. The HF 4x8 trailer without tires and wheels ships at 205 lbs and if it is like the one I bought from them, it is constructed of U channel, not tubular.

[purplepickup]

In April I had the dilema of using angle vs tube for my tongue too. http://tnttt.com/viewto ... t=meisters

I used 2X3X3/16 angle mostly because I already had it, but sort of against the advise of a few. After I welded it on I bounced it around a little and it just seemed a little too flexy for me. My trailer will be around 1100 lbs so I welded a cross piece of angle in and two pieces of 1.5X2X1/8 rectangular tubing going back into the main frame. Andrew's spreadsheet said the angle was probably safe but marginal. Since I do go way back in the boonies a lot, the extra pieces are just added insurance.

I'm pretty sure I could haul a bulldozer on it now but it added a lot of weight. I could have built a lighter tongue out of square tubing that would have been plenty strong. Sometimes my frugal (cheap) side gets in the way of my practical side.

[doug hodder]

hey guy...I really like the way you welded up the frame...I'm not one to cut corners and sweat out making it lighter, besides if you ever have any failure you at least have some material to weld to...I also didn't miter the corners on the frame...cut them at 90 and then cap...I think it just welds up a lot easier and not as much of a hassle getting it square. good job...I had a lot of flex in the tongue on mine also as I originally built it with 1.5 x 3 channel...I ended up boxing it......Doug Hodder

[cracker39]

Those additional support pieces welded onto the tongue would also be great for supporting a storage box. I think I may add that to my chassis plan, using only angle iron to conserve weight. Part of your flexing may have been due to so little of the tongue length welding under the front. I started with only 10" under the frame due to a drop down floor, but I remove the dropdown and redesigned the ends of the tongue to go back about 18" or maybe even more under the frame before welding in place. At the moment, I've measured them at 6' each, with the hitch coupler about 4-4.5 feet from the base of the cabin (which extends up and forward about 10"). That would end up with the cabin front 3-3.5 ft from the ball.

I once built a small boat trailer that had a single piece of 2" tube for the tongue, not sure of the wall thickness now. The chassis started out as a 4'x6' utility trailer and the tongue was bolted on with at least 6 ft from the chassis front to the hitch ball. It did flex a lot, but I never had a structural problem with it since the boat and trailer probably weighed no more than 500 lbs. I was able to pick up the tongue and move the whole thing around the yard.

[angib]

I've added to my tongue strength web page that the material to look for is 'Hot Rolled' steel. At both Online Metals and Metals Depot, this will get you A36 steel which is a decent structural grade.

Dale, I don't think any part of George's tongue flex would have been due to an insufficient connection with the rest of the frame. However I have seen some frames with the tongue member(s) connected only to the front-most cross-member and I have to say that scares me. Not only is the tongue cantilevered off a member that's behaving like a torsion bar (tube is good in torsion, but not that good....) but it's only got a small stress-raising connection.

Andrew

[AmyH]

Doug, this topic has been concerning me since you originally mentioned that you found the 1.5 X 3 channel too flexy (previous post). I am using the Kuffel Creek plans for the Comet, and Kevin calls for the use of 3/16" X 2" X 3" channel, which is what I bought and have sitting in my shop ready to weld up. Do you think that this is going to be too flexy, and if so what would your recommendation be? I want to make sure that after putting all this effort into building my tear that it will last.

Amy

[Cutterpup]

Amy, We used 2 x 2 1/8 square tube for our comet and it has been okay. Kevin tends to overbuild, and just about everybody on this board that has had a problem can be traced to over use or over loaded. If you are going to tow the trailer over unimproved roads or dirt trails the 3/16 2 x 3 channel might be a little small if you travel over normal roads without overloading the trailer it will be okay. BTW if my trailer breakes I built it and I can fix it!

Dan

[AmyH]

Thanks for the info Dan, I have been questioning whether I should just pick up some more 2x2x1/8 tubing to use for the tongue. I may occasionally want to take the tear on some bumpy roads, so I would rather build it for those conditions. There is definitely something to be said about building it all yourself, because then you really should be able to fix it if it breaks, but I would rather have it last then have major issues that need to be fixed. I would like to "get it right" the first time, if possible.

Amy

[angib]

Kevin calls for the use of 3/16" X 2" X 3" channel, which is what I bought and have sitting in my shop ready to weld up. Do you think that this is going to be too flexy, and if so what would your recommendation be?

Amy,

I've added your channel to the list on my tongue strength page - it's stronger than just about everything else listed there and more than twice as strong as the 2" x 2" x 1/8" tube you mention. So swapping the channel for anything else will make your frame weaker!

For the anal among us, the strength of this channel compared to its weight is impressive (2.3 times as strong as the 1/8" tube, but only 1.4 times the weight) - a good reminder of why our grandfathers came up with channel.

Andrew